Using the App
Interactive Key Search
Interactive Fret Search
Interactive Key Slider
Scope & “Why?”s
Pitch & Intervals
Musical Objects
Clocks & Pitch Classes
Grouping Clocks
Equivalence Groups
Evenness & Clusters
Orbifold & Voice Leading
A Diatonic Puzzle
Beyond Diatonic
Staff Notation
Circle of Fifths & Keys
Fret Diagrams
CAGED Fretboard System
Diatonic Modes & Chords
Extensions & Avoid Notes
Top-Down View
Leave-Out Notes
The Game
A Diatonic Puzzle
Theory
Where does the major or diatonic scale come from? And the pentatonic scale? Why have these two scales been rediscovered across so many cultures?
Do-Re-Mi-Fa-So-La-Ti-Do
The pentatonic scale—and its complement, the diatonic or major scale—are two scales that are central to many human musical traditions. Where do these scales come from? And why have they been rediscovered across so many cultures? Is this the only corner of the musical landscape explored by humans?
Tap to hear a few octaves of the diatonic scale played (the white keys), followed by a few octaves of the pentatonic scale (the black keys).
In order to explore what makes these two scales special, let’s step out of the narrow five- or seven-note collections and look at the entire 12-tone chromatic scale as a whole.
Fresh Perspective: A Puzzle
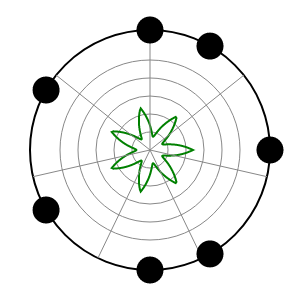
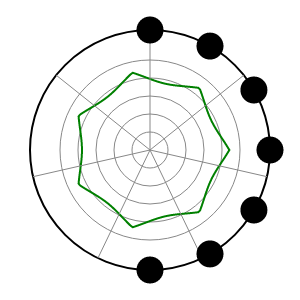
You are tasked with seating seven guests at a table with twelve evenly-spaced, permanently bolted-down chairs. The question is: what seating arrangement seats the guests at the table maximally far from one another, or maximally evenly?
For example, here are some poor solutions to the problem, as the guests are seated quite unevenly:
The Solution
If you make some attempt at moving the guests around, you may find a few answers that seem like candidate solutions, but there is a single unique solution. Click or tap here to spoil the puzzle and see the solution. (If you pay attention, you may notice that the title of this article gives away the answer.)
Other possible seating arrangements may seem nearly correct, but we can test the possibilities exhaustively and find out mathematically which one is the most even, by comparing the distance to a table with seven evenly spaced seats (corresponding to 7-TET).
An example of a fairly even set class, the Harmonic Major scale (left) and an example of a quite uneven set class Chromatic-7 (right). See Evenness & Clusters for more about evenness.
Analogy Explained
The twelve chairs are analogous to the twelve tones of the chromatic (equal-tempered) scale, and the maximally even seating plan is analogous to the diatonic collection of notes, or major scale. (For an explanation of where the chromatic scale comes from, see Pitch & Intervals.) The guests seated next to one another are akin to a semitone, and gaps between guests containing an empty chair are akin to a whole-tone.
The diatonic scale is a unique solution to the mathematical problem of making a collection of notes where we depart from any one specific starting note, take seven short steps, and return to the same note an octave higher or lower, and do so in the smoothest possible manner (short steps) that is also non-trivial (not boring like the chromatic scale).
The diatonic scale is also a unique solution to the problem of how to make twelve related major scales (same relative seating plan, but at twelve different angles) that share six of their seven notes with related scales (circle of fifths, analogous to having one specific guest move by one seat to the next empty chair, and maintaining the same exact maximal evenness and indeed the same, but rotated, seating plan).
Another Puzzle: Five Guests
We could pose another related puzzle. What about the most even seating plan for five guests and twelve chairs? If you have been paying attention, you may find other clues lurking on this page. Click or tap here to spoil the puzzle and see the solution.
Why is the Diatonic Scale Special?
Q. Why Does It Sound Good?
A. Because it has an interesting mix of mostly consonant intervals with some dissonant intervals, yet it is not too regular or boring (compare chromatic scale, whole-tone scale, diminished scale, augmented scale).
Q. Why Is It So Useful?
A. As we discussed in this section, it is maximally even (for cardinality equal to seven), so it is related to its transpositions by short voice leadings (a single semitone). This means major scales can be used for modulation, or for borrowing chromatic material from neighboring keys, without sounding “wrong.”
Q. What Else Is Even Possible?
A. If we accept that the diatonic scale is special for the reasons outlined above, what else is possible? What other scales share some of the same traits? That will be the subject of the next section.
Where does the major or diatonic scale come from? And the pentatonic scale? Why have these two scales been rediscovered across so many cultures?
Do-Re-Mi-Fa-So-La-Ti-Do
The pentatonic scale—and its complement, the diatonic or major scale—are two scales that are central to many human musical traditions. Where do these scales come from? And why have they been rediscovered across so many cultures? Is this the only corner of the musical landscape explored by humans?
Tap to hear a few octaves of the diatonic scale played (the white keys), followed by a few octaves of the pentatonic scale (the black keys).
In order to explore what makes these two scales special, let’s step out of the narrow five- or seven-note collections and look at the entire 12-tone chromatic scale as a whole.
Fresh Perspective: A Puzzle
You are tasked with seating seven guests at a table with twelve evenly-spaced, permanently bolted-down chairs. The question is: what seating arrangement seats the guests at the table maximally far from one another, or maximally evenly?
For example, here are some poor solutions to the problem, as the guests are seated quite unevenly:
The Solution
If you make some attempt at moving the guests around, you may find a few answers that seem like candidate solutions, but there is a single unique solution. Click or tap here to spoil the puzzle and see the solution. (If you pay attention, you may notice that the title of this article gives away the answer.)
Other possible seating arrangements may seem nearly correct, but we can test the possibilities exhaustively and find out mathematically which one is the most even, by comparing the distance to a table with seven evenly spaced seats (corresponding to 7-TET).
An example of a fairly even set class, the Harmonic Major scale (left) and an example of a quite uneven set class Chromatic-7 (right). See Evenness & Clusters for more about evenness.
Analogy Explained
The twelve chairs are analogous to the twelve tones of the chromatic (equal-tempered) scale, and the maximally even seating plan is analogous to the diatonic collection of notes, or major scale. (For an explanation of where the chromatic scale comes from, see Pitch & Intervals.) The guests seated next to one another are akin to a semitone, and gaps between guests containing an empty chair are akin to a whole-tone.
The diatonic scale is a unique solution to the mathematical problem of making a collection of notes where we depart from any one specific starting note, take seven short steps, and return to the same note an octave higher or lower, and do so in the smoothest possible manner (short steps) that is also non-trivial (not boring like the chromatic scale).
The diatonic scale is also a unique solution to the problem of how to make twelve related major scales (same relative seating plan, but at twelve different angles) that share six of their seven notes with related scales (circle of fifths, analogous to having one specific guest move by one seat to the next empty chair, and maintaining the same exact maximal evenness and indeed the same, but rotated, seating plan).
Another Puzzle: Five Guests
We could pose another related puzzle. What about the most even seating plan for five guests and twelve chairs? If you have been paying attention, you may find other clues lurking on this page. Click or tap here to spoil the puzzle and see the solution.
Why is the Diatonic Scale Special?
Q. Why Does It Sound Good?
A. Because it has an interesting mix of mostly consonant intervals with some dissonant intervals, yet it is not too regular or boring (compare chromatic scale, whole-tone scale, diminished scale, augmented scale).
Q. Why Is It So Useful?
A. As we discussed in this section, it is maximally even (for cardinality equal to seven), so it is related to its transpositions by short voice leadings (a single semitone). This means major scales can be used for modulation, or for borrowing chromatic material from neighboring keys, without sounding “wrong.”
Q. What Else Is Even Possible?
A. If we accept that the diatonic scale is special for the reasons outlined above, what else is possible? What other scales share some of the same traits? That will be the subject of the next section.
