Using the App
Interactive Key Search
Interactive Fret Search
Interactive Key Slider
Scope & “Why?”s
Pitch & Intervals
Musical Objects
Clocks & Pitch Classes
Grouping Clocks
Equivalence Groups
Evenness & Clusters
Orbifold & Voice Leading
A Diatonic Puzzle
Beyond Diatonic
Staff Notation
Circle of Fifths & Keys
Fret Diagrams
CAGED Fretboard System
Diatonic Modes & Chords
Extensions & Avoid Notes
Top-Down View
Leave-Out Notes
The Game
Diatonic Modes & Chords
Theory
After introducing staff notation and keys, music theory traditionally begins with tertiary harmony, which just means chords built from stacked major and minor thirds. Explanations often start with the diatonic or major scale.
Diatonic Modes
First we start with the white keys, the major or diatonic scale, in the Key of C Major, but this analysis applies to all keys, and C Major is in no way theoretically special, just from a notation point of view (and instrument-building), it is easier to explain.
Each note of the C Major scale, 
starting with C, is given a Roman numeral:
I
ii
iii
IV
V
vi
vii
C
D
E
F
G
A
B
In addition to the major mode ( Do-Re-Mi-Fa-So-La-Ti-Do), we can extract seven modes from the diatonic scale, with fancy Greek names for each mode, starting and ending on each possible note, as follows:
1, 2, 3, 4, 5, 6, 7, 1
I
C, D, E, F, G, A, B, C
C Ionian
(the major mode)
ii
D, E, F, G, A, B, C, D
D Dorian
(a minor mode)
iii
E, F, G, A, B, C, D, E
E Phrygian
(a dark, minor mode)
IV
F, G, A, B, C, D, E, F
F Lydian
(a bright major mode)
V
G, A, B, C, D, E, F, G
G Mixolydian
(a dark major mode)
vi
A, B, C, D, E, F, G, A
A Aeolian
(the natural minor mode)
vii
B, C, D, E, F, G, A, B
B Locrian
(a dark, diminished mode)
1, 2, 3, 4, 5, 6, 7, 1
Each note of each mode is assigned a decimal number 1 through 7 relative to the starting note, and instead of 8 for the octave, we get the number 1 again (see octave-equivalence). Here the note numbered 1 in each case is called the root because other notes are measured by their distance above this note, and because modes and chords will be named after the root.
The main point of Roman numeral function (functional analysis) is that all of the theory works the same for all keys (see transposition). (See Interactive Key Slider and Keys for a breakdown of all chords in all keys, with everything labeled with Roman numerals.)
Diatonic Triads
Now we can use these scales as material for building chords. For each mode, if we pick just the odd-numbered notes, we produce the major, minor and diminished triads:
I
1 3 5
C E G
R 3 5
C Major Triad
ii
1 3 5
D F A
R ♭3 5
D Minor Triad
iii
1 3 5
E G B
R ♭3 5
E Minor Triad
IV
1 3 5
F A C
R 3 5
F Major Triad
V
1 3 5
G B D
R 3 5
G Major Triad
vi
1 3 5
A C E
R ♭3 5
A Minor Triad
vii
1 3 5
B D F
R ♭3 ♭5
B Diminished Triad
The second column contains the scale degrees, but the fourth column contains the chord formula. To obtain these, we count semitones between the notes (see the intervals table for a list of all of these). From the root (R) to itself is zero semitones. From the root to a major third (3) is four semitones. From the root to a minor third (♭3) is three semitones. From the root to a perfect fifth (5) is seven semitones. From the root to a diminished fifth (♭5, a tritone) is six semitones.
Chords, especially triads, are usually explained as “coming from” odd scale degrees (more below) of the modes of the diatonic scale, but it is important to remember that alternate explanations (such as the exhaustive, musical set theory approach) show that triads are not special except in that they are nearly even, as are other chords and scales. All chord and scale types are their own thing, and exist independently, inherent to the mathematical and musical theoretic structure of the chromatic scale. (See Clocks & Pitch Classes for the long explanation.)
This example shows both the advantage and disadvantage of explaining diatonic modes and chords from the point of view of the piano keyboard, with its C-major focus: counting notes and scale degrees is easy, but counting in semitones is not so readily apparent (must include black keys—staff notation obscures this info). Other keyboard designs of real manufactured instruments exist that allow chord formula shapes to be seen clearly, and reused across modes and chords with any root, such as the isomorphic keyboard (including the accordion), or the Jankó keyboard. The guitar is also an instrument where generally chord shapes are preserved across transposition. See CAGED Fretboard System.
Now that we know which Roman numerals correspond to major and minor triads (and major and minor modes), we see why some are capitalized (major) or lowercase (minor), with lowercase plus degree symbol () standing for a diminished triad.
Diatonic Seventh Chords
Extending this approach to notes of odd scale degrees above the fifth, we get seventh chords:
I
1 3 5 7
C E G B
R 3 5 7
C Major Seventh
ii
1 3 5 7
D F A C
R ♭3 5 ♭7
D Minor Seventh
iii
1 3 5 7
E G B D
R ♭3 5 ♭7
E Minor Seventh
IV
1 3 5 7
F A C E
R 3 5 7
F Major Seventh
V
1 3 5 7
G B D F
R 3 5 ♭7
G Dominant Seventh
vi
1 3 5 7
A C E G
R ♭3 5 ♭7
A Minor Seventh
vii
1 3 5 7
B D F A
R ♭3 ♭5 ♭7
B Minor Seventh ♭5
(Half-Diminished Seventh)
We will discuss how to construct chords from the even scale degrees in a later section, where 2, 4, and 6 become 9, 11, and 13, intervals above the octave.
Currently we have collected up the following information:
I
C Maj
C Maj 7
C Ionian (Major)
ii
D min
D min 7
D Dorian
iii
E min
E min 7
E Phrygian
IV
F Maj
F Maj 7
F Lydian
V
G Maj
G Dom 7
G Mixolydian
vi
A min
A min 7
A Aeolian (Natural Minor)
vii
B dim
B min 7 ♭5
B Locrian
We can also look at the formula for each type of triad and seventh chord in terms of third intervals, one note to the next:
Augmented Triad
R 3 5
Major Third, Major Third
Major Triad
R 3 5
Major Third, Minor Third
Minor Triad
R ♭3 5
Minor Third, Major Third
Diminished Triad
R ♭3 ♭5
Minor Third, Minor Third
Major Seventh
R 3 5 7
Major Third, Minor Third, Major Third
Dominant Seventh
R 3 5 ♭7
Major Third, Minor Third, Minor Third
Minor Seventh
R ♭3 5 ♭7
Minor Third, Major Third, Minor Third
Minor Seventh ♭5 (Half-Diminished)
R ♭3 ♭5 ♭7
Minor Third, Minor Third, Major Third
Another View of Modes
Modes can be confusing because there is a second way of looking at them. Here we keep C as the root, and extract modes (notes) from seven different major scales (unordered sets of notes, basically the notes of a major key), ordered by keys on the circle of fifths:
IV
C Lydian
(a bright major mode)
C D E F G A B C
from the
Key of G
I
C Ionian
(Major)
C D E F G A B C
from the
Key of C
V
C Mixolydian
(a dark major mode)
C D E F G A B♭ C
from the
Key of F
ii
C Dorian
(a minor mode)
C D E♭ F G A B♭ C
from the
Key of B♭
vi
C Aeolian
(the natural minor mode)
C D E♭ F G A♭ B♭ C
from the
Key of E♭
iii
C Phrygian
(a dark, minor mode)
C D♭ E♭ F G A♭ B♭ C
from the
Key of A♭
vii
C Locrian
(diminished mode)
C D♭ E♭ F G♭ A♭ B♭ C
from the
Key of D♭
We see that each mode shares six of seven notes with each neighbor.
Diatonic Circle of Fifths
This ordering of vii - iii - vi - ii - V - I - IV - vii - ... is called the diatonic circle of fifths, showing the fifths (or fourths) relationships between the roots of the triads within a key, for example C Major:
IV
F Maj
F A C
3 semitones apart,
2 scale steps away
F A C ⟺ E G C
I
C Maj
C E G
3 semitones apart,
2 scale steps away
C E G ⟺ B D G
V
G Maj
G B D
4 semitones apart,
2 scale steps away
G B D ⟺ F A D
ii
D min
D F A
3 semitones apart,
2 scale steps away
D F A ⟺ C E A
vi
A min
A C E
3 semitones apart,
2 scale steps away
A C E ⟺ G B E
iii
E min
E G B
4 semitones apart,
2 scale steps away
E G B ⟺ D F B
vii
B dim
B D F
4 semitones apart,
2 scale steps away
B D F ⟺ A C F
IV
F Maj
F A C
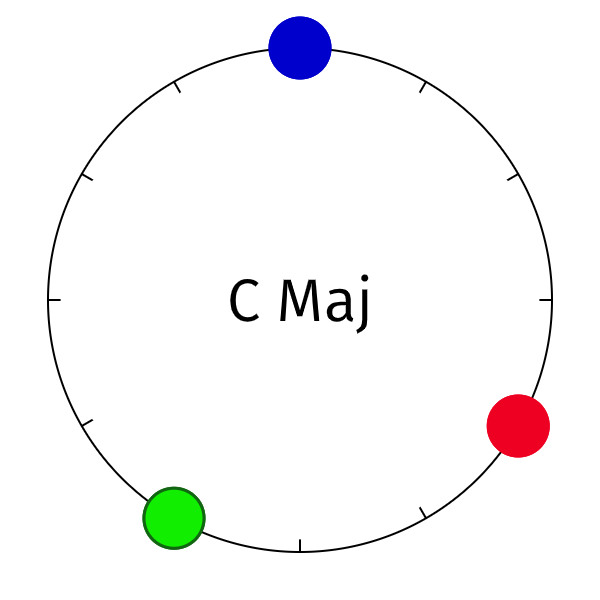
This animation demonstrates many short voice-leadings between neighboring pairs of chords, but note that it does not demonstrate every short voice leading between diatonic triads, for example F Maj and D min.
Diatonic Circle of Thirds
Tymoczko 2011 §6.3.2 shows a more useful circle of triads, the diatonic circle of thirds, where each triad in a given key is placed in sequence with the two triads that are the closest in terms of short voice-leading distance. The root of each chord is one diatonic third (major or minor third) away from the root of its neighbor.
I
C Maj
C E G
2 semitones apart,
1 scale step away
C E G ⟺ C E A
vi
A min
A C E
1 semitone apart,
1 scale step away
A C E ⟺ A C F
IV
F Maj
F A C
2 semitones apart,
1 scale step away
F A C ⟺ F A D
ii
D min
D F A
2 semitones apart,
1 scale step away
B D F ⟺ A D F
vii
B dim
B D F
2 semitones apart,
1 scale step away
B D F ⟺ B D G
V
G Maj
G B D
2 semitones apart,
1 scale step away
E G B ⟺ D G B
iii
E min
E G B
1 semitone apart,
1 scale step away
C E G ⟺ B E G
I
C Maj
C E G
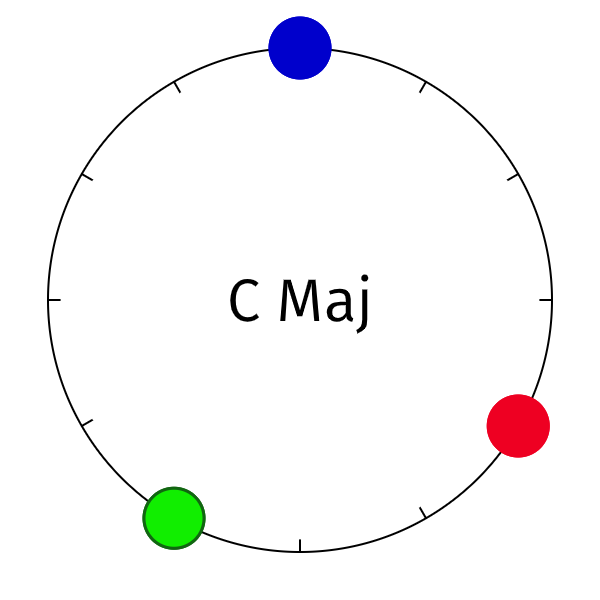
The main point is that the shortest voice leading between diatonic triads in the same key will be composed of one or more turns (in one direction) on this circle of thirds. (An exercise for the reader is to try to decompose the voice leadings between chords on the circle of fifths above.)
(See the Interactive Key Slider on the page for Key of C Major for another way to visualize the relationships between chords in this key, which essentially reproduces the circle of thirds.)
Now we have seen how the modes of the diatonic scale can be used as construction materials for chords. What if we were to generalize this to intervals above the seventh, such as 9, 11, and 13, and to all modes and all chords? That is the topic of the next sections.
After introducing staff notation and keys, music theory traditionally begins with tertiary harmony, which just means chords built from stacked major and minor thirds. Explanations often start with the diatonic or major scale.
Diatonic Modes
First we start with the white keys, the major or diatonic scale, in the Key of C Major, but this analysis applies to all keys, and C Major is in no way theoretically special, just from a notation point of view (and instrument-building), it is easier to explain.
Each note of the C Major scale, starting with C, is given a Roman numeral:
| I | ii | iii | IV | V | vi | vii |
| C | D | E | F | G | A | B |
In addition to the major mode ( Do-Re-Mi-Fa-So-La-Ti-Do), we can extract seven modes from the diatonic scale, with fancy Greek names for each mode, starting and ending on each possible note, as follows:
| 1, 2, 3, 4, 5, 6, 7, 1 | |||
| I | C, D, E, F, G, A, B, C | |
C Ionian (the major mode) |
| ii | D, E, F, G, A, B, C, D | |
D Dorian (a minor mode) |
| iii | E, F, G, A, B, C, D, E | |
E Phrygian (a dark, minor mode) |
| IV | F, G, A, B, C, D, E, F | |
F Lydian (a bright major mode) |
| V | G, A, B, C, D, E, F, G | |
G Mixolydian (a dark major mode) |
| vi | A, B, C, D, E, F, G, A | |
A Aeolian (the natural minor mode) |
| vii | B, C, D, E, F, G, A, B | |
B Locrian (a dark, diminished mode) |
| 1, 2, 3, 4, 5, 6, 7, 1 |
Each note of each mode is assigned a decimal number 1 through 7 relative to the starting note, and instead of 8 for the octave, we get the number 1 again (see octave-equivalence). Here the note numbered 1 in each case is called the root because other notes are measured by their distance above this note, and because modes and chords will be named after the root.
The main point of Roman numeral function (functional analysis) is that all of the theory works the same for all keys (see transposition). (See Interactive Key Slider and Keys for a breakdown of all chords in all keys, with everything labeled with Roman numerals.)
Diatonic Triads
Now we can use these scales as material for building chords. For each mode, if we pick just the odd-numbered notes, we produce the major, minor and diminished triads:
| I | 1 3 5 | C E G |
R 3 5 | C Major Triad |
| ii | 1 3 5 | D F A |
R ♭3 5 | D Minor Triad |
| iii | 1 3 5 | E G B |
R ♭3 5 | E Minor Triad |
| IV | 1 3 5 | F A C |
R 3 5 | F Major Triad |
| V | 1 3 5 | G B D |
R 3 5 | G Major Triad |
| vi | 1 3 5 | A C E |
R ♭3 5 | A Minor Triad |
| vii | 1 3 5 | B D F |
R ♭3 ♭5 | B Diminished Triad |
The second column contains the scale degrees, but the fourth column contains the chord formula. To obtain these, we count semitones between the notes (see the intervals table for a list of all of these). From the root (R) to itself is zero semitones. From the root to a major third (3) is four semitones. From the root to a minor third (♭3) is three semitones. From the root to a perfect fifth (5) is seven semitones. From the root to a diminished fifth (♭5, a tritone) is six semitones.
Chords, especially triads, are usually explained as “coming from” odd scale degrees (more below) of the modes of the diatonic scale, but it is important to remember that alternate explanations (such as the exhaustive, musical set theory approach) show that triads are not special except in that they are nearly even, as are other chords and scales. All chord and scale types are their own thing, and exist independently, inherent to the mathematical and musical theoretic structure of the chromatic scale. (See Clocks & Pitch Classes for the long explanation.)
This example shows both the advantage and disadvantage of explaining diatonic modes and chords from the point of view of the piano keyboard, with its C-major focus: counting notes and scale degrees is easy, but counting in semitones is not so readily apparent (must include black keys—staff notation obscures this info). Other keyboard designs of real manufactured instruments exist that allow chord formula shapes to be seen clearly, and reused across modes and chords with any root, such as the isomorphic keyboard (including the accordion), or the Jankó keyboard. The guitar is also an instrument where generally chord shapes are preserved across transposition. See CAGED Fretboard System.
Now that we know which Roman numerals correspond to major and minor triads (and major and minor modes), we see why some are capitalized (major) or lowercase (minor), with lowercase plus degree symbol () standing for a diminished triad.
Diatonic Seventh Chords
Extending this approach to notes of odd scale degrees above the fifth, we get seventh chords:
| I | 1 3 5 7 | C E G B |
R 3 5 7 | C Major Seventh |
| ii | 1 3 5 7 | D F A C |
R ♭3 5 ♭7 | D Minor Seventh |
| iii | 1 3 5 7 | E G B D |
R ♭3 5 ♭7 | E Minor Seventh |
| IV | 1 3 5 7 | F A C E |
R 3 5 7 | F Major Seventh |
| V | 1 3 5 7 | G B D F |
R 3 5 ♭7 | G Dominant Seventh |
| vi | 1 3 5 7 | A C E G |
R ♭3 5 ♭7 | A Minor Seventh |
| vii | 1 3 5 7 | B D F A |
R ♭3 ♭5 ♭7 | B Minor Seventh ♭5 (Half-Diminished Seventh) |
We will discuss how to construct chords from the even scale degrees in a later section, where 2, 4, and 6 become 9, 11, and 13, intervals above the octave.
Currently we have collected up the following information:
| I | C Maj | C Maj 7 | C Ionian (Major) |
| ii | D min | D min 7 | D Dorian |
| iii | E min | E min 7 | E Phrygian |
| IV | F Maj | F Maj 7 | F Lydian |
| V | G Maj | G Dom 7 | G Mixolydian |
| vi | A min | A min 7 | A Aeolian (Natural Minor) |
| vii | B dim | B min 7 ♭5 | B Locrian |
We can also look at the formula for each type of triad and seventh chord in terms of third intervals, one note to the next:
| Augmented Triad | R 3 5 | Major Third, Major Third |
| Major Triad | R 3 5 | Major Third, Minor Third |
| Minor Triad | R ♭3 5 | Minor Third, Major Third |
| Diminished Triad | R ♭3 ♭5 | Minor Third, Minor Third |
| Major Seventh | R 3 5 7 | Major Third, Minor Third, Major Third |
| Dominant Seventh | R 3 5 ♭7 | Major Third, Minor Third, Minor Third |
| Minor Seventh | R ♭3 5 ♭7 | Minor Third, Major Third, Minor Third |
| Minor Seventh ♭5 (Half-Diminished) | R ♭3 ♭5 ♭7 | Minor Third, Minor Third, Major Third |
Another View of Modes
Modes can be confusing because there is a second way of looking at them. Here we keep C as the root, and extract modes (notes) from seven different major scales (unordered sets of notes, basically the notes of a major key), ordered by keys on the circle of fifths:
| IV | C Lydian (a bright major mode) |
C D E F G A B C | |
from the Key of G |
| I | C Ionian (Major) |
C D E F G A B C | |
from the Key of C |
| V | C Mixolydian (a dark major mode) |
C D E F G A B♭ C | |
from the Key of F |
| ii | C Dorian (a minor mode) |
C D E♭ F G A B♭ C | |
from the Key of B♭ |
| vi | C Aeolian (the natural minor mode) |
C D E♭ F G A♭ B♭ C | |
from the Key of E♭ |
| iii | C Phrygian (a dark, minor mode) |
C D♭ E♭ F G A♭ B♭ C | |
from the Key of A♭ |
| vii | C Locrian (diminished mode) |
C D♭ E♭ F G♭ A♭ B♭ C | |
from the Key of D♭ |
We see that each mode shares six of seven notes with each neighbor.
Diatonic Circle of Fifths
This ordering of vii - iii - vi - ii - V - I - IV - vii - ... is called the diatonic circle of fifths, showing the fifths (or fourths) relationships between the roots of the triads within a key, for example C Major:
| IV | F Maj | F A C |
| 3 semitones apart, 2 scale steps away |
F A C ⟺ E G C | |
| I | C Maj | C E G |
| 3 semitones apart, 2 scale steps away |
C E G ⟺ B D G | |
| V | G Maj | G B D |
| 4 semitones apart, 2 scale steps away |
G B D ⟺ F A D | |
| ii | D min | D F A |
| 3 semitones apart, 2 scale steps away |
D F A ⟺ C E A | |
| vi | A min | A C E |
| 3 semitones apart, 2 scale steps away |
A C E ⟺ G B E | |
| iii | E min | E G B |
| 4 semitones apart, 2 scale steps away |
E G B ⟺ D F B | |
| vii | B dim | B D F |
| 4 semitones apart, 2 scale steps away |
B D F ⟺ A C F | |
| IV | F Maj | F A C |
This animation demonstrates many short voice-leadings between neighboring pairs of chords, but note that it does not demonstrate every short voice leading between diatonic triads, for example F Maj and D min.
Diatonic Circle of Thirds
Tymoczko 2011 §6.3.2 shows a more useful circle of triads, the diatonic circle of thirds, where each triad in a given key is placed in sequence with the two triads that are the closest in terms of short voice-leading distance. The root of each chord is one diatonic third (major or minor third) away from the root of its neighbor.
| I | C Maj | C E G |
| 2 semitones apart, 1 scale step away |
C E G ⟺ C E A | |
| vi | A min | A C E |
| 1 semitone apart, 1 scale step away |
A C E ⟺ A C F | |
| IV | F Maj | F A C |
| 2 semitones apart, 1 scale step away |
F A C ⟺ F A D | |
| ii | D min | D F A |
| 2 semitones apart, 1 scale step away |
B D F ⟺ A D F | |
| vii | B dim | B D F |
| 2 semitones apart, 1 scale step away |
B D F ⟺ B D G | |
| V | G Maj | G B D |
| 2 semitones apart, 1 scale step away |
E G B ⟺ D G B | |
| iii | E min | E G B |
| 1 semitone apart, 1 scale step away |
C E G ⟺ B E G | |
| I | C Maj | C E G |
The main point is that the shortest voice leading between diatonic triads in the same key will be composed of one or more turns (in one direction) on this circle of thirds. (An exercise for the reader is to try to decompose the voice leadings between chords on the circle of fifths above.)
(See the Interactive Key Slider on the page for Key of C Major for another way to visualize the relationships between chords in this key, which essentially reproduces the circle of thirds.)
Now we have seen how the modes of the diatonic scale can be used as construction materials for chords. What if we were to generalize this to intervals above the seventh, such as 9, 11, and 13, and to all modes and all chords? That is the topic of the next sections.
