Clocks & Pitch Classes
Theory
4,096 pitch class sets capture every possible musical object, and let us see some important connections between objects by visualizing any chord or scale on a circle.
Pitch Classes
A pitch class is the collection of all notes with the same name, one or more octaves apart. In 12-TET, there are twelve pitch classes, conventionally named with numbers starting from zero.
- C
- C# or D♭
- D
- D# or E♭
- E
- F
- F# or G♭
- G
- G# or A♭
- A
- (or t for ten). A# or B♭
- (or e for eleven). B

Start with the 88-key piano as a number line, going from the first, lowest note on the left side of the piano to the last, highest note on the right, including both black and white keys. The twelve pitch classes  are represented visually here by circles of the same color.
are represented visually here by circles of the same color.

Octave equivalence turns linear pitch space into a spiral. Ignoring duplicates of notes in the same pitch class (cardinality-equivalence) and flattening that spiral into a circle gives us pitch class sets (which also ignores the order of the notes, permutation-equivalence).
Pitch Class Sets: Colored Clock Diagrams
A pitch class set (not to be confused with a set class, covered in the next section) is a musical object represented by the answer to twelve yes/no questions, relating just the presence or absence of each pitch class without regard to octave register or note duplication: does the chord or scale have at least one C note? a C#/D♭ note? D? D#/E♭? E, etc.

This is represented visually by filled (colored) circles or dots at twelve clock locations when the answer for that pitch class is yes, and an empty white circle when the answer is no. Arbitrarily, C is placed at the top (twelve o'clock) and D is clockwise from there at two o'clock, etc. * The colors are also arbitrary, but loosely based on the work of ex-color-blind cyborg and futurist Neil Harbisson. The dots are drawn here as large, touching circles to make them more visible at small sizes, but in the actual, circular, continuous pitch-class space, the dots are 30º apart (= 360º ÷ 12, in 12-TET).






Example pitch class sets. Top row:  C Maj,
C Maj,  C min. Center row:
C min. Center row:  the white keys or C Major (Diatonic),
the white keys or C Major (Diatonic),  G Major (Diatonic). Bottom row:
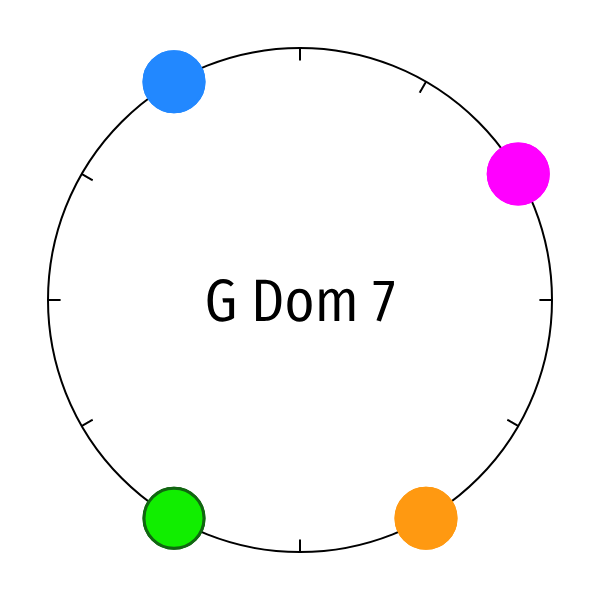
G Major (Diatonic). Bottom row:  G Dom 7,
G Dom 7,  D♭ Dom 7.
D♭ Dom 7.
Cardinality
An important concept in musical set theory is cardinality. This just means the number of distinct pitch classes, as opposed to the number of notes in a scale or chord.


The top examples  have three notes and four notes, but both have cardinality of three, since the C note is duplicated. The bottom examples
have three notes and four notes, but both have cardinality of three, since the C note is duplicated. The bottom examples  have seven and eight notes, but with duplicate C note treated the same as a single C note, they both have cardinality of seven.
have seven and eight notes, but with duplicate C note treated the same as a single C note, they both have cardinality of seven.
Harmonious focuses on chords and scales with cardinality three to nine.* Cardinality zero is silence, cardinality one is just the individual notes of the chromatic scale, cardinality two is just the intervals, and cardinality ten and eleven are just the chromatic scale missing a few notes, like walking over to a piano and lying one’s forearm on most of the notes simultaneously. Not very interesting harmonically.
All Possible Pitch Class Sets
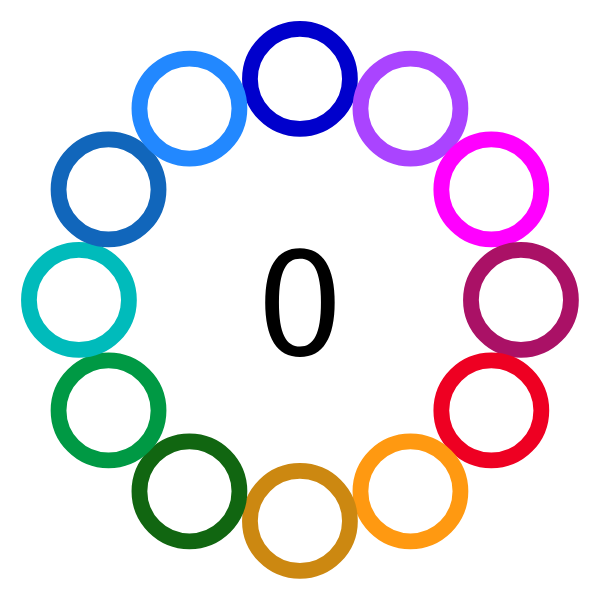
Mathematically, there are two possibilities per pitch class (yes and no), so there are 2 × 2 × 2 ... 2 = 212 = 4,096 possible pitch class sets. This includes all of the objects we care about:* This also includes: 1× 12-note chromatic scale (12-TET) and 1× 0-note silence, 12× individual notes, 66× transpositions of the 2-note intervals, 66× 10-note scales and 12× 11-note scales (just the chromatic scale missing a note or two). all of the 3-note chords and scale fragments, all 4-, 5- and 6-note chords/scales, and all 7-, 8- and 9-note scales. (What’s more, we can enumerate them all by simply counting in binary, as in the above animation!)
Find any piece of music, old or new, and any chord or scale from the piece can be reduced to a pitch class set which will be on the list of 4,096.
Voice Leading
Pitch class sets let us compare two colored clocks and understand how they may relate geometrically, in terms of shared notes and voice leading, a topic for another section.
The next section will use transposition to group colored clocks into black and white clocks, (a class of pitch class sets, or a set class) and then further group clock diagrams into fewer elements.
4,096 pitch class sets capture every possible musical object, and let us see some important connections between objects by visualizing any chord or scale on a circle.
Pitch Classes
A pitch class is the collection of all notes with the same name, one or more octaves apart. In 12-TET, there are twelve pitch classes, conventionally named with numbers starting from zero.
- C
- C# or D♭
- D
- D# or E♭
- E
- F
- F# or G♭
- G
- G# or A♭
- A
- (or t for ten). A# or B♭
- (or e for eleven). B
Start with the 88-key piano as a number line, going from the first, lowest note on the left side of the piano to the last, highest note on the right, including both black and white keys. The twelve pitch classes are represented visually here by circles of the same color.

Octave equivalence turns linear pitch space into a spiral. Ignoring duplicates of notes in the same pitch class (cardinality-equivalence) and flattening that spiral into a circle gives us pitch class sets (which also ignores the order of the notes, permutation-equivalence).
Pitch Class Sets: Colored Clock Diagrams
A pitch class set (not to be confused with a set class, covered in the next section) is a musical object represented by the answer to twelve yes/no questions, relating just the presence or absence of each pitch class without regard to octave register or note duplication: does the chord or scale have at least one C note? a C#/D♭ note? D? D#/E♭? E, etc.

This is represented visually by filled (colored) circles or dots at twelve clock locations when the answer for that pitch class is yes, and an empty white circle when the answer is no. Arbitrarily, C is placed at the top (twelve o'clock) and D is clockwise from there at two o'clock, etc. * The colors are also arbitrary, but loosely based on the work of ex-color-blind cyborg and futurist Neil Harbisson. The dots are drawn here as large, touching circles to make them more visible at small sizes, but in the actual, circular, continuous pitch-class space, the dots are 30º apart (= 360º ÷ 12, in 12-TET).
Example pitch class sets. Top row: C Maj,
C min. Center row:
the white keys or C Major (Diatonic),
G Major (Diatonic). Bottom row:
G Dom 7,
D♭ Dom 7.
Cardinality
An important concept in musical set theory is cardinality. This just means the number of distinct pitch classes, as opposed to the number of notes in a scale or chord.
The top examples have three notes and four notes, but both have cardinality of three, since the C note is duplicated. The bottom examples
have seven and eight notes, but with duplicate C note treated the same as a single C note, they both have cardinality of seven.
Harmonious focuses on chords and scales with cardinality three to nine.* Cardinality zero is silence, cardinality one is just the individual notes of the chromatic scale, cardinality two is just the intervals, and cardinality ten and eleven are just the chromatic scale missing a few notes, like walking over to a piano and lying one’s forearm on most of the notes simultaneously. Not very interesting harmonically.
All Possible Pitch Class Sets

Mathematically, there are two possibilities per pitch class (yes and no), so there are 2 × 2 × 2 ... 2 = 212 = 4,096 possible pitch class sets. This includes all of the objects we care about:* This also includes: 1× 12-note chromatic scale (12-TET) and 1× 0-note silence, 12× individual notes, 66× transpositions of the 2-note intervals, 66× 10-note scales and 12× 11-note scales (just the chromatic scale missing a note or two). all of the 3-note chords and scale fragments, all 4-, 5- and 6-note chords/scales, and all 7-, 8- and 9-note scales. (What’s more, we can enumerate them all by simply counting in binary, as in the above animation!)
Find any piece of music, old or new, and any chord or scale from the piece can be reduced to a pitch class set which will be on the list of 4,096.
Voice Leading
Pitch class sets let us compare two colored clocks and understand how they may relate geometrically, in terms of shared notes and voice leading, a topic for another section.

The next section will use transposition to group colored clocks into black and white clocks, (a class of pitch class sets, or a set class) and then further group clock diagrams into fewer elements.