Using the App
Interactive Key Search
Interactive Fret Search
Interactive Key Slider
Scope & “Why?”s
Pitch & Intervals
Musical Objects
Clocks & Pitch Classes
Grouping Clocks
Equivalence Groups
Evenness & Clusters
Orbifold & Voice Leading
A Diatonic Puzzle
Beyond Diatonic
Staff Notation
Circle of Fifths & Keys
Fret Diagrams
CAGED Fretboard System
Diatonic Modes & Chords
Extensions & Avoid Notes
Top-Down View
Leave-Out Notes
The Game
Grouping Clocks
Theory
Grouping up to twelve transpositions of colored clock diagrams into a single black and white clock diagram (a set class) leaves us with 336 set classes, which cover every conceivable chord or scale. Grouping clocks a few more ways brings the number down even further.
Set Classes: Black and White Clock Diagrams
Start with any colored clock and rotate it by one position, then repeat this twelve times, to generate up to twelve rotations or transpositions. The position we use to represent or name the group of all twelve colored clocks is the “lowest numerical representation,” or prime form.
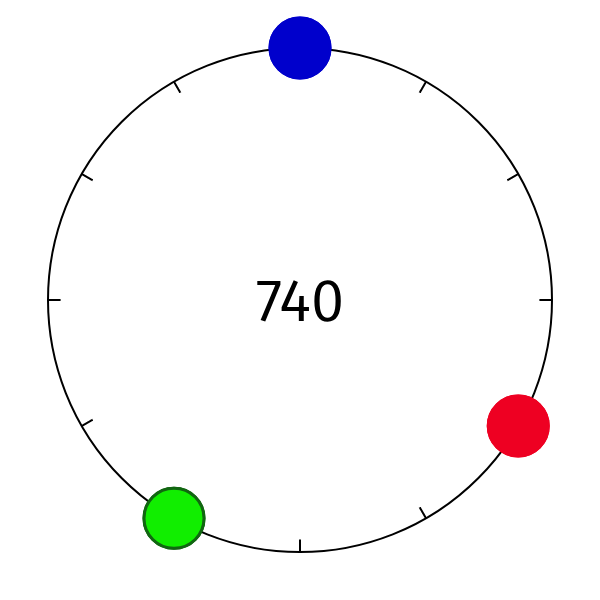
For example, 
in this animation of all of the transpositions of the major triad, the lowest numerical representation is 740* In base twelve, but this works like any familiar positional number system such as base ten, with the most significant digit on the left and the least significant on the right. but we follow the convention laid out by Allen Forte and write it (047).
This diagram is (047), a black and white clock in prime form, the set class that collects the twelve transpositions of the major triad into a single object.
Modes of Limited Transposition
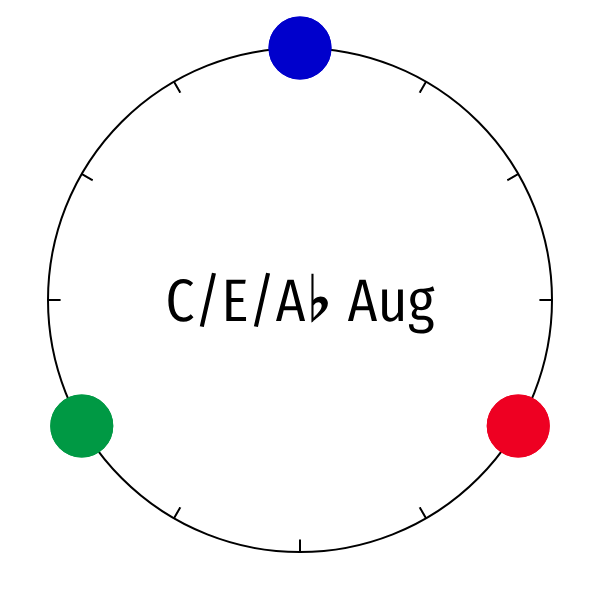
In this animation, we see that it repeats after only four unique pitch class sets. (The augmented triad is a mode of limited transposition.)
The number in the middle of a clock diagram, ×12, or ×4, tells us how many unique pitch class set objects it collects into one named object, where the name (the prime form) is the lowest representation, e.g. (047) for major triads, and (048) for augmented triads.
All Possible Set Classes
In this animation, if we run through all 4,096 colored clock diagrams as before, and just keep the clocks with the lowest numerical representation, shown in black, leaving the rest light gray, we count 350 black-and-white clock diagrams (or 336 of cardinality three to nine).
Evenness & Involution
Black and white clock diagrams let us compare the evenness of different clocks, a topic discussed in detail in a later section.
We can see that if we flip a clock on its axis (like looking at a clock from behind), the interval relationships (and evenness) are preserved. This lets us see when two set classes are related by involution, another way to group musical objects into fewer elemental groups.
The most common example of a pair of set classes related by involution (but not by transposition) is the major triad (047) and the minor triad (037), together grouped with Forte number 3-11. They share all of the same intervals, but in a different order: major third, minor third, perfect fifth. (Note also that if we flip a set class, there may be some rotation (transposition) required to get the involuted (flipped) set class into prime form. In fact, the animation above is one of the few pairs of involuted set classes where this is not the case.)
Symmetry
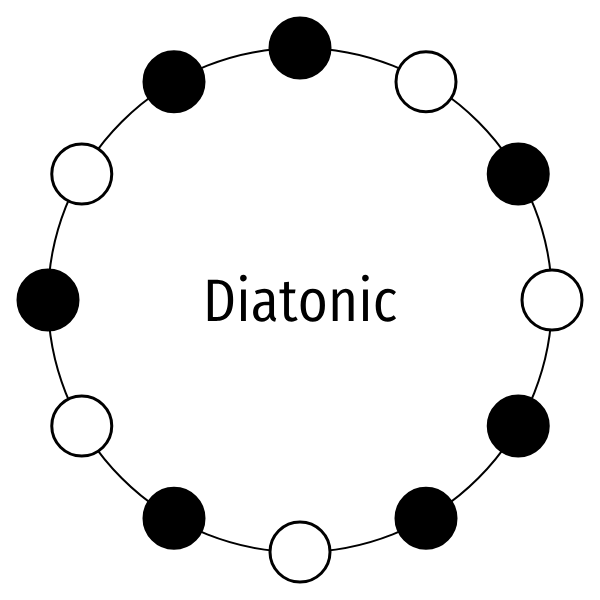
If a set class is related to itself by involution and transposition, it is considered symmetric. For example, the diatonic scale is symmetric: if we flip it and rotate it a bit, it is still the diatonic scale.
Complementarity
The last transformation we can do to a clock (aside from rotating and flipping) is to toggle each pitch class.
In the above animation, we can see that if we make a new copy of a clock, with each pitch class toggled, that is, remove a circle where one exists, and add one where one is missing, we preserve the shape of the set class, because we can repeat another toggle and get back the original clock diagram.
Two set classes related in this way are complements, a transformation that captures a deep and important relationship between set classes, and provides the last rule for grouping set classes together.
This image of a piano keyboard shows how the black keys (pentatonic scale) and the white keys (diatonic scale) on a piano are related: the holes or gaps in one preserve the shape of the notes in the other (the white keys with the black keys considered the “holes”, or vice versa).
Notice also how the pentatonic scale is just a subset of the diatonic scale. (In fact all 3-, 4-, and 5-note set classes are always a subset of their 9-, 8-, and 7-note complements!)* Ian Quinn’s masters thesis on Q-space (see References) describes in more detail the importance of complementarity and the mathematics behind set classes which are complements.
“Elements” of Musical Set Theory
Now we are at the end of the journey to find out how many ways we can group objects together, and hence, how many possible chords and scales there are, reduced to their “elements.”
Grouping
# (card. 0 to 12)
# (card. 3 to 9)
Colored Clocks
4,096
3,938
Black & White Clocks
350
336
By Involution
222
208
By Complementarity
122
115
In chemistry, no element in nature or the laboratory falls outside the periodic table of 118 elements. In musical set theory, no chord or scale of cardinality three to nine falls outside the 115 rows of the set classes tables.
Precision Terminology for Grouping (and Naming) Things
The next section will discuss terminology related to transposition, involution, and complementarity and quantify some upper bounds on the number of possible chords and scales.
Grouping up to twelve transpositions of colored clock diagrams into a single black and white clock diagram (a set class) leaves us with 336 set classes, which cover every conceivable chord or scale. Grouping clocks a few more ways brings the number down even further.
Set Classes: Black and White Clock Diagrams
Start with any colored clock and rotate it by one position, then repeat this twelve times, to generate up to twelve rotations or transpositions. The position we use to represent or name the group of all twelve colored clocks is the “lowest numerical representation,” or prime form.
For example, in this animation of all of the transpositions of the major triad, the lowest numerical representation is 740* In base twelve, but this works like any familiar positional number system such as base ten, with the most significant digit on the left and the least significant on the right. but we follow the convention laid out by Allen Forte and write it (047).
This diagram is (047), a black and white clock in prime form, the set class that collects the twelve transpositions of the major triad into a single object.
Modes of Limited Transposition
In this animation, we see that it repeats after only four unique pitch class sets. (The augmented triad is a mode of limited transposition.)
The number in the middle of a clock diagram, ×12, or ×4, tells us how many unique pitch class set objects it collects into one named object, where the name (the prime form) is the lowest representation, e.g. (047) for major triads, and (048) for augmented triads.
All Possible Set Classes
In this animation, if we run through all 4,096 colored clock diagrams as before, and just keep the clocks with the lowest numerical representation, shown in black, leaving the rest light gray, we count 350 black-and-white clock diagrams (or 336 of cardinality three to nine).
Evenness & Involution
Black and white clock diagrams let us compare the evenness of different clocks, a topic discussed in detail in a later section.
We can see that if we flip a clock on its axis (like looking at a clock from behind), the interval relationships (and evenness) are preserved. This lets us see when two set classes are related by involution, another way to group musical objects into fewer elemental groups.
The most common example of a pair of set classes related by involution (but not by transposition) is the major triad (047) and the minor triad (037), together grouped with Forte number 3-11. They share all of the same intervals, but in a different order: major third, minor third, perfect fifth. (Note also that if we flip a set class, there may be some rotation (transposition) required to get the involuted (flipped) set class into prime form. In fact, the animation above is one of the few pairs of involuted set classes where this is not the case.)
Symmetry
If a set class is related to itself by involution and transposition, it is considered symmetric. For example, the diatonic scale is symmetric: if we flip it and rotate it a bit, it is still the diatonic scale.
Complementarity
The last transformation we can do to a clock (aside from rotating and flipping) is to toggle each pitch class.
In the above animation, we can see that if we make a new copy of a clock, with each pitch class toggled, that is, remove a circle where one exists, and add one where one is missing, we preserve the shape of the set class, because we can repeat another toggle and get back the original clock diagram.
Two set classes related in this way are complements, a transformation that captures a deep and important relationship between set classes, and provides the last rule for grouping set classes together.
This image of a piano keyboard shows how the black keys (pentatonic scale) and the white keys (diatonic scale) on a piano are related: the holes or gaps in one preserve the shape of the notes in the other (the white keys with the black keys considered the “holes”, or vice versa).
Notice also how the pentatonic scale is just a subset of the diatonic scale. (In fact all 3-, 4-, and 5-note set classes are always a subset of their 9-, 8-, and 7-note complements!)* Ian Quinn’s masters thesis on Q-space (see References) describes in more detail the importance of complementarity and the mathematics behind set classes which are complements.
“Elements” of Musical Set Theory
Now we are at the end of the journey to find out how many ways we can group objects together, and hence, how many possible chords and scales there are, reduced to their “elements.”
| Grouping | # (card. 0 to 12) | # (card. 3 to 9) |
|---|---|---|
| Colored Clocks | 4,096 | 3,938 |
| Black & White Clocks | 350 | 336 |
| By Involution | 222 | 208 |
| By Complementarity | 122 | 115 |
In chemistry, no element in nature or the laboratory falls outside the periodic table of 118 elements. In musical set theory, no chord or scale of cardinality three to nine falls outside the 115 rows of the set classes tables.
Precision Terminology for Grouping (and Naming) Things
The next section will discuss terminology related to transposition, involution, and complementarity and quantify some upper bounds on the number of possible chords and scales.
