Circle of Fifths & Keys
Theory
The circle of fifths refers to the twelve transpositions of the diatonic scale (also key or major scale) ordered so that each scale differs from its neighbors by a single note. The root or name of each major scale is related to its neighbors by either a fourth or fifth.
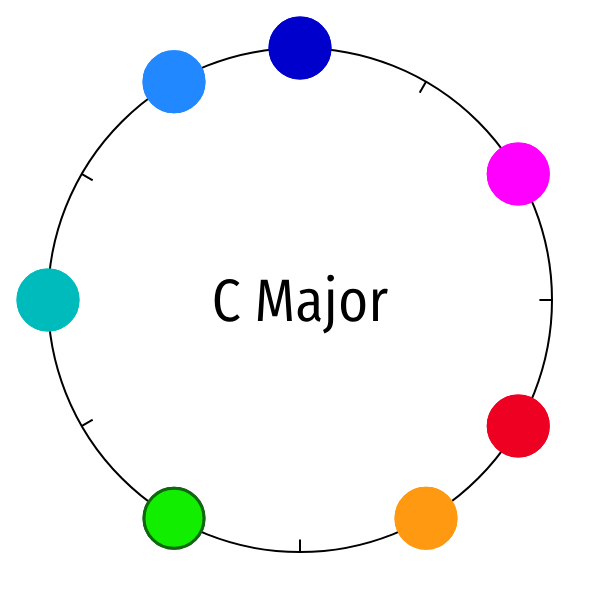
The term circle of fourths can also be used, meaning: up a fifth, which is octave-equivalent to down a fourth; or a up a fourth, which is octave-equivalent to down a fifth, depending on the direction. The circle can be involuted and the relationships are preserved since perfect fourths and fifths share an interval class.


The circle of fourths is the same sequence as the circle of fifths, just going in the opposite direction. In these  two diagrams of a keyboard, the sequence of colored dots (note names) is the same but
two diagrams of a keyboard, the sequence of colored dots (note names) is the same but  reversed.
reversed.
There is also a minor key circle of fifths (below).
Keys
Major-minor tonality in the common practice is organized into twelve major keys and twelve minor keys. Each key collects up a set of chords and progressions which emphasizes movement away from and back to the tonic, a chord sharing the name of the key.
All keys share Roman numeral function, which reduces the information about how chords within keys are related to one another by a factor of twelve, via transposition.
(See Keys index page for links to all the keys.)

There are fifteen major and fifteen minor named keys for historical tuning reasons (before the advent of twelve-tone equal temperament) and as a quirk of musical notation. In twelve-tone equal temperament, three keys have two names and two sets of notation. These three keys are considered six different keys in historical tuning systems, where instruments were tuned in such a way as to limit each piece of music to a small number of keys.
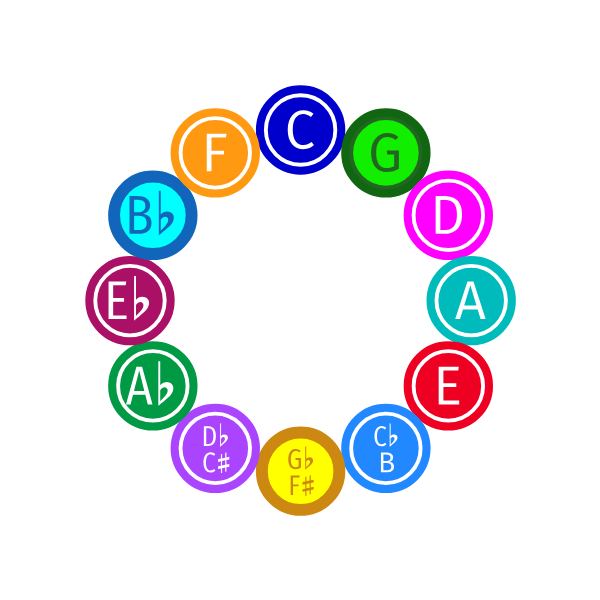
This shows the major circle of fourths, and how it is the same sequence as the circle of fifths above, just mirrored or reversed. The animated lines show fourths and fifths, going out from the note C to notes 5 or 7 steps away on the circle, repeatedly, until we arrive one tritone away, at F#. (The fact that the same transformation converts the circle of fifths to the circle of semitones and back demonstrates the M-relation.)
Minor Circle of Fifths
The natural minor mode for each diatonic transposition follows a similar naming order, so the minor circle of fifths is rotated three steps. The key of C major has the same signature as the key of A minor, etc.

It is important to remember that the minor circle of fifths is basically the same twelve unordered collections of seven notes, just with different labels. (There is some subtlety since the concept of a minor scale or a minor key is an ambiguous term.)
Before Eating A Donut, Get Coffee First
A useful mnemonic for remembering the sequence B, E, A, D, G, C, F is “Before Eating A Donut, Get Coffee First.”
The same sequence in reverse is F, C, G, D, A, E, B, which can be remembered with the phrase “Forgo Chocolate Glazed Donuts And Eat Breakfast.”
In the circle diagram above, the sequence of key names starting with the key of B (5 sharps) is as follows:
… … 
Key of C

Key of F

Key of B 
Key of E 
Key of A 
Key of D 
Key of G 
Key of C 
Key of F 
Key of B♭ 
Key of E♭ 
Key of A♭ 
Key of D♭ = C

Key of G♭ = F

Key of C♭ = B 
Key of F♭ = E … …
The same sequence also describes the order in which sharps and flats are added (or removed) as you move around the circle of fifths:



- B, E, A, D, G, C, F (from seven sharps, the Key of C down to one sharp, the Key of G)
- B♭, E♭, A♭, D♭, G♭, C♭, F♭ (from one flat, the Key of F, up to seven flats, the Key of C♭)

This jargon and notation may seem a bit complicated (a downside of historical musical notation), but the arithmetic or geometric concepts underlying the labels is actually simple enough to understand when viewed on a circle as an animation. Try not to lose sight of that beauty, simplicity, and symmetry: semitone voice leading between unordered collections of seven maximally evenly spaced notes—transpositions (all notes rotated exactly 5 or 7 semitones) of a single pattern of intervals, the diatonic scale.
The circle of fifths refers to the twelve transpositions of the diatonic scale (also key or major scale) ordered so that each scale differs from its neighbors by a single note. The root or name of each major scale is related to its neighbors by either a fourth or fifth.

The term circle of fourths can also be used, meaning: up a fifth, which is octave-equivalent to down a fourth; or a up a fourth, which is octave-equivalent to down a fifth, depending on the direction. The circle can be involuted and the relationships are preserved since perfect fourths and fifths share an interval class.
The circle of fourths is the same sequence as the circle of fifths, just going in the opposite direction. In these two diagrams of a keyboard, the sequence of colored dots (note names) is the same but
reversed.
There is also a minor key circle of fifths (below).
Keys
Major-minor tonality in the common practice is organized into twelve major keys and twelve minor keys. Each key collects up a set of chords and progressions which emphasizes movement away from and back to the tonic, a chord sharing the name of the key.
All keys share Roman numeral function, which reduces the information about how chords within keys are related to one another by a factor of twelve, via transposition.
(See Keys index page for links to all the keys.)
There are fifteen major and fifteen minor named keys for historical tuning reasons (before the advent of twelve-tone equal temperament) and as a quirk of musical notation. In twelve-tone equal temperament, three keys have two names and two sets of notation. These three keys are considered six different keys in historical tuning systems, where instruments were tuned in such a way as to limit each piece of music to a small number of keys.

This shows the major circle of fourths, and how it is the same sequence as the circle of fifths above, just mirrored or reversed. The animated lines show fourths and fifths, going out from the note C to notes 5 or 7 steps away on the circle, repeatedly, until we arrive one tritone away, at F#. (The fact that the same transformation converts the circle of fifths to the circle of semitones and back demonstrates the M-relation.)
Minor Circle of Fifths
The natural minor mode for each diatonic transposition follows a similar naming order, so the minor circle of fifths is rotated three steps. The key of C major has the same signature as the key of A minor, etc.
It is important to remember that the minor circle of fifths is basically the same twelve unordered collections of seven notes, just with different labels. (There is some subtlety since the concept of a minor scale or a minor key is an ambiguous term.)
Before Eating A Donut, Get Coffee First
A useful mnemonic for remembering the sequence B, E, A, D, G, C, F is “Before Eating A Donut, Get Coffee First.”
The same sequence in reverse is F, C, G, D, A, E, B, which can be remembered with the phrase “Forgo Chocolate Glazed Donuts And Eat Breakfast.”
In the circle diagram above, the sequence of key names starting with the key of B (5 sharps) is as follows:
| … | … |
| Key of C | |
| Key of F | |
| Key of B | |
| Key of E | |
| Key of A | |
| Key of D | |
| Key of G | |
| Key of C | |
| Key of F | |
| Key of B♭ | |
| Key of E♭ | |
| Key of A♭ | |
| Key of D♭ = C | |
| Key of G♭ = F | |
| Key of C♭ = B | |
| Key of F♭ = E | |
| … | … |
The same sequence also describes the order in which sharps and flats are added (or removed) as you move around the circle of fifths:


- B, E, A, D, G, C, F (from seven sharps, the Key of C down to one sharp, the Key of G)
- B♭, E♭, A♭, D♭, G♭, C♭, F♭ (from one flat, the Key of F, up to seven flats, the Key of C♭)

This jargon and notation may seem a bit complicated (a downside of historical musical notation), but the arithmetic or geometric concepts underlying the labels is actually simple enough to understand when viewed on a circle as an animation. Try not to lose sight of that beauty, simplicity, and symmetry: semitone voice leading between unordered collections of seven maximally evenly spaced notes—transpositions (all notes rotated exactly 5 or 7 semitones) of a single pattern of intervals, the diatonic scale.