Using the App
Interactive Key Search
Interactive Fret Search
Interactive Key Slider
Scope & “Why?”s
Pitch & Intervals
Musical Objects
Clocks & Pitch Classes
Grouping Clocks
Equivalence Groups
Evenness & Clusters
Orbifold & Voice Leading
A Diatonic Puzzle
Beyond Diatonic
Staff Notation
Circle of Fifths & Keys
Fret Diagrams
CAGED Fretboard System
Diatonic Modes & Chords
Extensions & Avoid Notes
Top-Down View
Leave-Out Notes
The Game
Evenness & Clusters
Theory
Take a high-level view of the set classes, with trends that show which areas of the tables are important (and why). One question asked at the beginning (Q2) will be answered: why are certain chords and scales so commonly used in practice?
Evenness
Here we will focus on the 208 OPTIC-equivalent set classes (grouped by Forte number), and attempt to cut that number down by more than half. Since black and white clocks have the same intervals and evenness when they are related by involution, this seems like a reasonable place to start. We have 208 of either of the following: (a) a single symmetric clock or (b) a pair of involution-equivalent clocks. Again, at this point we are still exhaustive: it is not possible to offer up a chord or scale within 12-TET that cannot be treated as one of these 208 set classes.
The augmented triad (top) is perfectly even, and major and minor triads (bottom) are nearly even.
Diatonic-3 (top) and Chromatic-3 (bottom) are very uneven set classes.
First we divide up the set classes by cardinality three through nine. For each set class, we determine its evenness, which can be measured by computing the minimum distance on the circle to the perfectly even C-note chord (where C is the cardinality). (For C = 5, C = 7, C = 8, or C = 9, this perfectly even chord cannot be found in 12-TET but is equal to 5-TET, 7-TET, 8-TET, and 9-TET respectively.)
An example of a fairly even set class, the Harmonic Major scale (left) and an example of a quite uneven set class, Chromatic-7 (right).
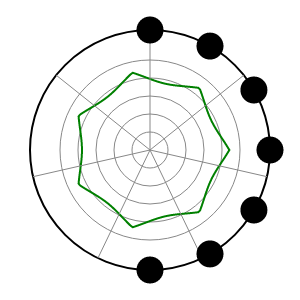
The Euclidean distance from the set class (black dots) to the perfectly even seven-note chord (lines) is shown in green on the radial plot (same scale as the rings in the evenness plot below). Low minimum distance to the perfectly even chord means higher evenness (a distance of zero is perfectly even), and higher minimum distance means lower evenness. These distance values can be found on the set classes table page and on the page for each set class.
Chromatic Clusters
A set class with a chromatic cluster, a run of three or more chromatic notes in a row (two or more consecutive semitone intervals), is said to be chromatic cluster-containing. These are marked with three or more gray circles—instead of black filled circles—on a black and white clock diagram.
A set class without chromatic clusters is said to be chromatic cluster-free.
Plotting by Evenness
Now we will take all of the set classes, grouped by cardinality, and plot them by evenness along seven line segments, labeled C = 3 through C = 9.
Here, a pair of involution-equivalent set classes is shown by a shape with a double border. A single symmetric set class has a single border. Set classes that are modes of limited transposition are marked with a black dot in the center. Set classes that contain chromatic clusters are colored dark gray, and cluster-free set classes are filled light gray.
The top-left corner has three perfectly even chords for C = 3, C = 4, and C = 6 (since they are factors of twelve). The maximally even and nearly even chords surround them. (See By Evenness for details.)
The bottom and right outside edges have the seven chromatic runs of length three through nine. The different geometric shapes will be explained in a later section.
Trends
We immediately see some obvious trends across the space:
Center and left (red) Right and outside edges (blue)
More even More uneven
More likely cluster-free More likely to contain chromatic clusters
More chord-like More scale-like or scale-fragment-like
More tonal More chromatic, atonal
More voice-leading possibilities Fewer voice-leading possibilities, degenerate
More versatile, more useful, hence more common More of a harmonic dead-end
The Cluster-free Division
We can imagine a fairly clean line dividing the cluster-free set classes from the cluster-containing set classes. This group of cluster-free set classes contains all of the most common chords and scales (in the top-left corner) and all of the chords that can most easily change into other structurally similar chords by short voice leading.
Equivalence
# Card. 3 to 9
# Cluster-free
Octave
hundreds of thousands
tens of thousands
OC
23,628
6,720
OPC
3,938
1,420
OPTC
336
124
OPTIC
208
80
OPTIC/K
115
–
–
–
–
OTC
1,969
560
By ignoring chromatic cluster-containing set classes and focusing on cluster-free set classes, we have reduced the number of chords to explore substantially: we are down to 560 OTC-equivalent modes of 124 set classes (black and white clock diagrams) which will yield us tens of thousands of playable chords and scales, instead of hundreds of thousands. Further sections will group these hundreds of chord/scale types into just a handful of unordered scale types, and group chord types together under seventeen mode types, something much easier to keep track of.
We have shown that the most common chords and scales (across diverse styles of Western and even some non-Western music) are nearly even and mentioned that this correlates to the chord or scale’s ability to participate in voice leading. This answers Q2—why some chords and scales are so common—because of their usefulness in progressions (chords) or modulations (scales). In fact, there is a single mathematical space that links evenness and voice leading, the orbifold, the subject of the next section.
Take a high-level view of the set classes, with trends that show which areas of the tables are important (and why). One question asked at the beginning (Q2) will be answered: why are certain chords and scales so commonly used in practice?
Evenness
Here we will focus on the 208 OPTIC-equivalent set classes (grouped by Forte number), and attempt to cut that number down by more than half. Since black and white clocks have the same intervals and evenness when they are related by involution, this seems like a reasonable place to start. We have 208 of either of the following: (a) a single symmetric clock or (b) a pair of involution-equivalent clocks. Again, at this point we are still exhaustive: it is not possible to offer up a chord or scale within 12-TET that cannot be treated as one of these 208 set classes.
The augmented triad (top) is perfectly even, and major and minor triads (bottom) are nearly even.
Diatonic-3 (top) and Chromatic-3 (bottom) are very uneven set classes.
First we divide up the set classes by cardinality three through nine. For each set class, we determine its evenness, which can be measured by computing the minimum distance on the circle to the perfectly even C-note chord (where C is the cardinality). (For C = 5, C = 7, C = 8, or C = 9, this perfectly even chord cannot be found in 12-TET but is equal to 5-TET, 7-TET, 8-TET, and 9-TET respectively.)
An example of a fairly even set class, the Harmonic Major scale (left) and an example of a quite uneven set class, Chromatic-7 (right).
The Euclidean distance from the set class (black dots) to the perfectly even seven-note chord (lines) is shown in green on the radial plot (same scale as the rings in the evenness plot below). Low minimum distance to the perfectly even chord means higher evenness (a distance of zero is perfectly even), and higher minimum distance means lower evenness. These distance values can be found on the set classes table page and on the page for each set class.
Chromatic Clusters
A set class with a chromatic cluster, a run of three or more chromatic notes in a row (two or more consecutive semitone intervals), is said to be chromatic cluster-containing. These are marked with three or more gray circles—instead of black filled circles—on a black and white clock diagram.
A set class without chromatic clusters is said to be chromatic cluster-free.
Plotting by Evenness
Now we will take all of the set classes, grouped by cardinality, and plot them by evenness along seven line segments, labeled C = 3 through C = 9.
Here, a pair of involution-equivalent set classes is shown by a shape with a double border. A single symmetric set class has a single border. Set classes that are modes of limited transposition are marked with a black dot in the center. Set classes that contain chromatic clusters are colored dark gray, and cluster-free set classes are filled light gray.
The top-left corner has three perfectly even chords for C = 3, C = 4, and C = 6 (since they are factors of twelve). The maximally even and nearly even chords surround them. (See By Evenness for details.)
The bottom and right outside edges have the seven chromatic runs of length three through nine. The different geometric shapes will be explained in a later section.
Trends
We immediately see some obvious trends across the space:
| Center and left (red) | Right and outside edges (blue) |
|---|---|
| More even | More uneven |
| More likely cluster-free | More likely to contain chromatic clusters |
| More chord-like | More scale-like or scale-fragment-like |
| More tonal | More chromatic, atonal |
| More voice-leading possibilities | Fewer voice-leading possibilities, degenerate |
| More versatile, more useful, hence more common | More of a harmonic dead-end |
The Cluster-free Division
We can imagine a fairly clean line dividing the cluster-free set classes from the cluster-containing set classes. This group of cluster-free set classes contains all of the most common chords and scales (in the top-left corner) and all of the chords that can most easily change into other structurally similar chords by short voice leading.
| Equivalence | # Card. 3 to 9 | # Cluster-free |
|---|---|---|
| Octave | hundreds of thousands | tens of thousands |
| OC | 23,628 | 6,720 |
| OPC | 3,938 | 1,420 |
| OPTC | 336 | 124 |
| OPTIC | 208 | 80 |
| OPTIC/K | 115 | – |
| – | – | – |
| OTC | 1,969 | 560 |
By ignoring chromatic cluster-containing set classes and focusing on cluster-free set classes, we have reduced the number of chords to explore substantially: we are down to 560 OTC-equivalent modes of 124 set classes (black and white clock diagrams) which will yield us tens of thousands of playable chords and scales, instead of hundreds of thousands. Further sections will group these hundreds of chord/scale types into just a handful of unordered scale types, and group chord types together under seventeen mode types, something much easier to keep track of.
We have shown that the most common chords and scales (across diverse styles of Western and even some non-Western music) are nearly even and mentioned that this correlates to the chord or scale’s ability to participate in voice leading. This answers Q2—why some chords and scales are so common—because of their usefulness in progressions (chords) or modulations (scales). In fact, there is a single mathematical space that links evenness and voice leading, the orbifold, the subject of the next section.
