Glossary
Voice Leading
Glossary
Voice leading in western polyphonic music of the common practice refers to the motion of one or more notes or voices moving by (usually) small distances when one chord (formed by the notes of one or more instruments) “changes” into another chord.
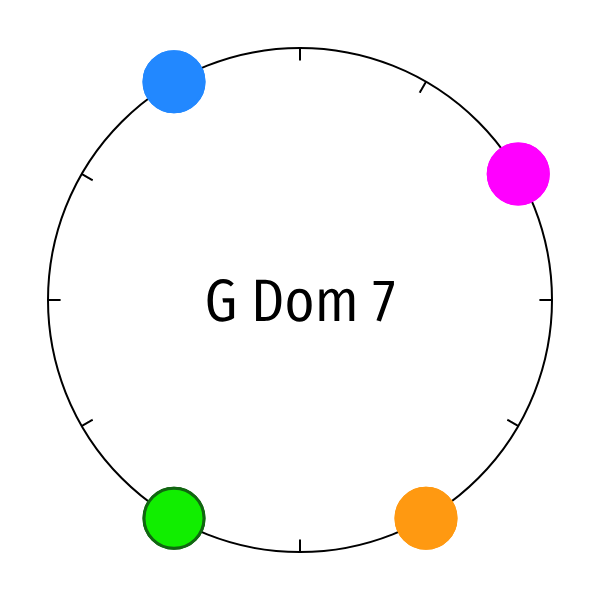
In the above animation, 
the note G (in green) is shared between both chords. There is a short (semitone) voice leading between E and F and back. The note B, the ♭7 of the G chord, resolves to the note C via another short voice leading. The D also resolves to the C, this time via a whole tone voice leading. (Notice how we don’t hear B resolving to E since the C is closer. Tymoczko 2006 emphasizes this concept of uncrossed voice leadings.)
The notion of voice-leading distance captures a lot of our intuition about chords sounding related to one another sequentially and progressions making sense harmonically, where short voice leadings sound good to our ears, and really long voice leadings don’t really seem like voice leadings at all, since they fail to connect seemingly unrelated chords.
This example of C minor leading into F major shows that the voice-leading distance between the two chords is longer than the distance between G Dom 7 and C Maj in the example at the top.
Tymoczko 2006 presents some criteria that capture this intuitive notion of voice-leading distance (the idea of uncrossed voice leadings; in the above example B doesn’t resolve to E because that makes no sense) and then presents an algorithm that can compute all possible voice leadings between two sets of pitch classes, including the shortest possible voice leading, using any reasonable definition of distance.
An important consequence of voice leading is that chords (and scales) that are more even (as long as they are not modes of limited transposition) are related to their own transpositions and involutions by short distances. (In fact there is a strong correlation between evenness and short voice-leading distance across all set classes.)
Tymoczko 2011 explains how to construct mathematically and visually a handful of related multi-dimensional spaces (one orbifold for each cardinality) in which all pitch class sets dwell in a lattice where lines connecting them represent a single-semitone voice leading, and the most even set classes are near the center of the space, with all chords of the same type placed the same distance from the center (exactly equal to their evenness), with degenerate sorts of chords far from the center.
See Evenness & Clusters for more about practical consequences of trends in the set classes.
Voice leading in western polyphonic music of the common practice refers to the motion of one or more notes or voices moving by (usually) small distances when one chord (formed by the notes of one or more instruments) “changes” into another chord.
In the above animation, the note G (in green) is shared between both chords. There is a short (semitone) voice leading between E and F and back. The note B, the ♭7 of the G chord, resolves to the note C via another short voice leading. The D also resolves to the C, this time via a whole tone voice leading. (Notice how we don’t hear B resolving to E since the C is closer. Tymoczko 2006 emphasizes this concept of uncrossed voice leadings.)
The notion of voice-leading distance captures a lot of our intuition about chords sounding related to one another sequentially and progressions making sense harmonically, where short voice leadings sound good to our ears, and really long voice leadings don’t really seem like voice leadings at all, since they fail to connect seemingly unrelated chords.
This example of C minor leading into F major shows that the voice-leading distance between the two chords is longer than the distance between G Dom 7 and C Maj in the example at the top.
Tymoczko 2006 presents some criteria that capture this intuitive notion of voice-leading distance (the idea of uncrossed voice leadings; in the above example B doesn’t resolve to E because that makes no sense) and then presents an algorithm that can compute all possible voice leadings between two sets of pitch classes, including the shortest possible voice leading, using any reasonable definition of distance.
An important consequence of voice leading is that chords (and scales) that are more even (as long as they are not modes of limited transposition) are related to their own transpositions and involutions by short distances. (In fact there is a strong correlation between evenness and short voice-leading distance across all set classes.)
Tymoczko 2011 explains how to construct mathematically and visually a handful of related multi-dimensional spaces (one orbifold for each cardinality) in which all pitch class sets dwell in a lattice where lines connecting them represent a single-semitone voice leading, and the most even set classes are near the center of the space, with all chords of the same type placed the same distance from the center (exactly equal to their evenness), with degenerate sorts of chords far from the center.
See Evenness & Clusters for more about practical consequences of trends in the set classes.