M-Relation
Glossary
Set Theory
Two set classes are M-related if they share the same interval content in the interval classes for whole-tone, minor third, major third, and tritone (equivalent to the FC2, FC3, FC4, FC6 components) but have semitones and fourths swapped. The “M” stands for Multiplication, referring to M5(y) and M7(y).
So for example the pentatonic scale and the five-note subset of the chromatic scale are M-related, since they have the same interval content for everything but semitones and fourths, which are swapped.
Many set classes are self-M-related, for example 6-Z12, (012467), which means replacing semitones with fourths results in the same set class. (Perhaps the set class has no semitone or fourth interval content, such as the augmented chord.)
The M-relation works on FC1 and FC5 (semitones and fourths) in 12-TET because 1 and 5 (or 11 and 7) are the generators of the cyclic group Z12, since 5, 7, and 11 are relatively prime to 12.
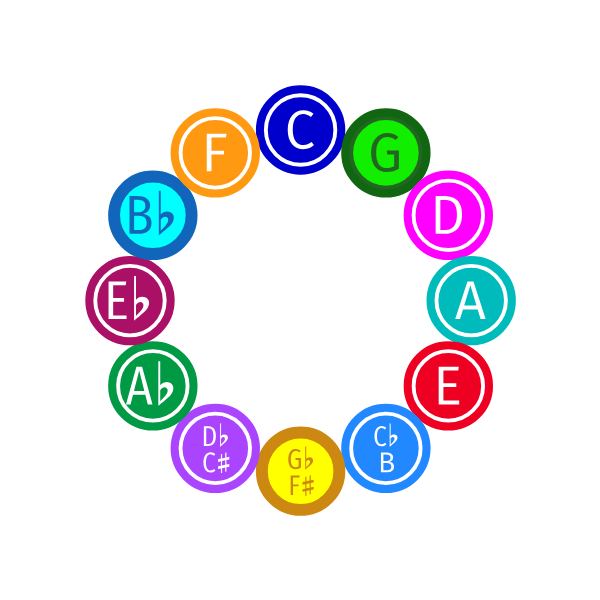
The animated lines show fourths and fifths, going out from the note C to notes 5 or 7 steps away on the circle, repeatedly, until we arrive one tritone away, at F#. The fact that the same transformation converts the circle of fifths to the circle of semitones and back demonstrates that the M-relation is its own inverse.
See also Z-Relation.
Set Theory
Two set classes are M-related if they share the same interval content in the interval classes for whole-tone, minor third, major third, and tritone (equivalent to the FC2, FC3, FC4, FC6 components) but have semitones and fourths swapped. The “M” stands for Multiplication, referring to M5(y) and M7(y).
So for example the pentatonic scale and the five-note subset of the chromatic scale are M-related, since they have the same interval content for everything but semitones and fourths, which are swapped.
Many set classes are self-M-related, for example 6-Z12, (012467), which means replacing semitones with fourths results in the same set class. (Perhaps the set class has no semitone or fourth interval content, such as the augmented chord.)
The M-relation works on FC1 and FC5 (semitones and fourths) in 12-TET because 1 and 5 (or 11 and 7) are the generators of the cyclic group Z12, since 5, 7, and 11 are relatively prime to 12.

The animated lines show fourths and fifths, going out from the note C to notes 5 or 7 steps away on the circle, repeatedly, until we arrive one tritone away, at F#. The fact that the same transformation converts the circle of fifths to the circle of semitones and back demonstrates that the M-relation is its own inverse.
See also Z-Relation.